유튜브에서 제공하는 이상엽 선생님의 강의를 정리한 것입니다.
https://www.youtube.com/watch?v=Q8NkThsTp_gh
핵심 내용
- 대수학의 대상: 수뿐만이 아니라 수를 대신할 수 있는 모든 것
- 대수학 = 대수구조를 연구하는 학문
- 대수구조 = 집합과 집합에 부여된 연산
- 다양한 대수구조:
- 반군(결합법칙)
- 모노이드(결합법칙, 항등원)
- 군(결합법칙, 항등원, 역원)
- 아벨군(결합법칙, 교환법칙, 항등원, 역원)
- 환(결합법칙, 교환법칙, 항등원, 역원 | 결합법칙)
- 가군
- 가환환(결합법칙, 교환법칙, 항등원, 역원 | 결합법칙, 교환법칙)
- 나눗셈환(결합법칙, 교환법칙, 항등원, 역원 | 결합법칙, 항등원, 역원)
- 체(결합법칙, 교환법칙, 항등원, 역원 | 결합법칙, 교환법칙, 항등원, 역원)
선형 대수는 대수학의 일부이다. 결론적으로 선형 대수학은 대수학의 일부로서 벡터 공간이라는 대수구조를 집중적으로 다루는 수학 분야이다. 벡터 공간을 중심으로 대수구조를 경험한다는 측면에서 대수학의 첫 발걸음이라고도 할 수 있다. 따라서 본격적인 선형 대수를 공부하기 전에, 선형 대수보다 넓은 범위의 대수학을 이해한다.
(1) 대수구조
대수학은 대수구조를 연구하는 학문이다. 대수학을 이해하기 위해서는 대수구조를 공부한다.
대수구조? - 집합 + 구조(연산, 공리)
대수학의 대수(代數)는 '수를 대신한다'는 의미를 가지고 있다. 이는 대수학이 '수' 뿐만 아니라 '수를 대신할 수 있는 모든 것'을 연구한다는 것을 말한다.
대수학에는 수뿐만 아니라 수를 대신할 수 있는 모든 것을 집합으로 간주한다. 대수구조는 이렇게 형성된 집합에 구조를 부여한 것이다. 구조는 사실상 연산이다. 집합 내 원소 사이에 연산을 정의하고, 이러한 연산이 가지는 공리도 구조에 포함한다.
종합하여 말하면 대수학은 대수구조를 다루는 학문이고, 대수구조는 수 또는 수를 대신할 수 있는 모든 것으로 구성한 집합과 집합에 정의된 연산이라고 할 수 있다.
(2) 여러 대수구조
대수학에서 다루는 대수구조는 다양하다. 특히 선형대수에서 다루는 벡터 역시 벡터 공간이라는 대수구조의 원소이다. 다양한 대수구조와 관계를 살펴본다.
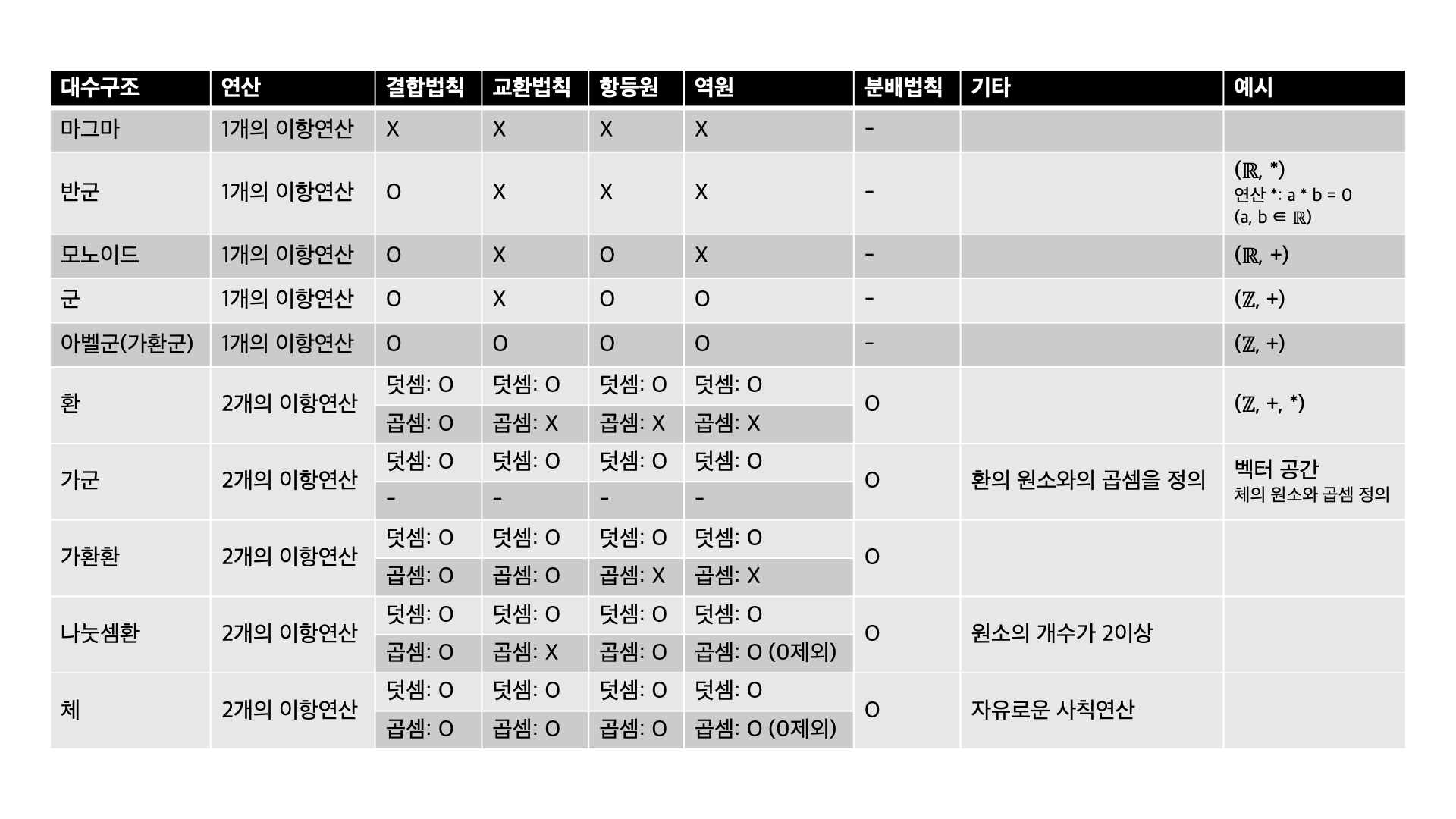
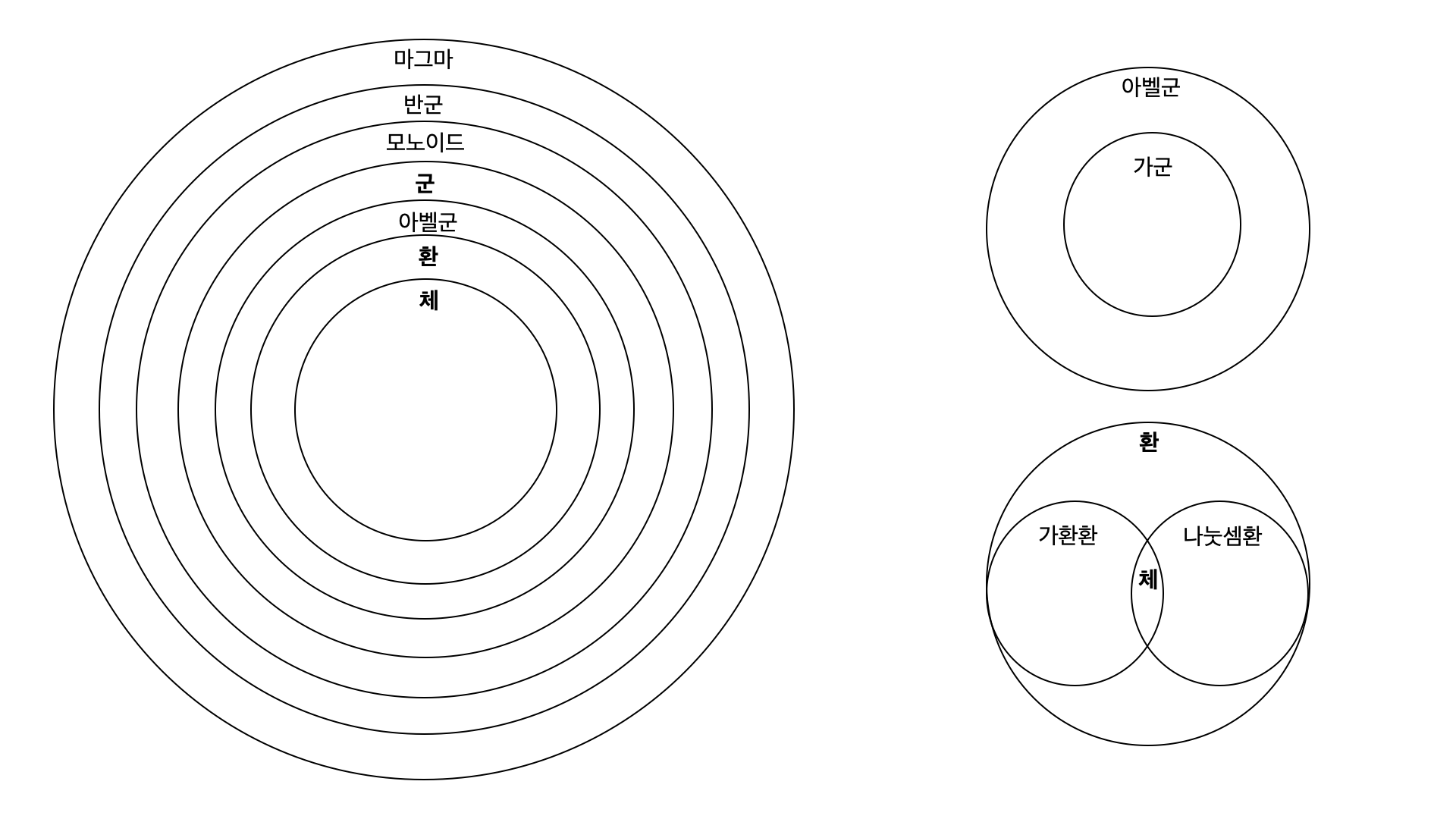
① 마그마(magma)
대수구조 마그마는 가장 상위의 대수구조이다. 집합에 대해 이항연산이 정의되어 있다면 마그마에 속할 수 있다. 정의된 이항연산은 연산법칙(교환법칙, 결합법칙)을 따르지 않아도 된다. 그저 집합에 속한 두 원소를 연산한 결과가 집합에 속하면(이항연산에 대해 닫혀있으면) 충분하다.
② 반군(semi group)
대수구조 반군은 집합과 그 위에 결합법칙을 따르는 하나의 이항연산을 갖춘 대수구조이다.
연산은 임의로 정의할 수 있다. 예를 들어 정수 집합 Z에 대해서 이항연산 *의 결과가 항상 0이라고 정의하자. 그렇다면 (Z, *)는 반군에 속하는 대수구조가 된다. 정수 집합에 속하는 임의의 원소 a, b, c에 대해서 (a * b) * c = a * (b * c) = 0 이므로 연산 *는 정수 집합 Z에 대해서 결합법칙을 만족한다.
③ 모노이드(monoid)
대수구조 모노이드는 항등원을 갖는 반군이다. 즉, 집합과 집합 위에 결합법칙을 만족하는 이항연산이 정의되어 있고, 이항연산에 대해서는 항등원이 존재한다.
위에서 반군에 속한 대수구조 (Z, *)는 모노이드에 속하지 못한다. 항등원은 연산의 결과가 자기 자신이 되어야하지만 정의한 연산 *는 임의의 정수 집합 원소에 대해서 항상 0이 결과로 나온다. a * x = a 를 만족하는 항등원 x는 존재하지 않으므로 (Z, *)는 모노이드에 속하지 않는다.
모노이드에 속하는 대수구조는 정수집합 Z에 정의된 덧셈(+) 연산이다. 덧셈은 기본적으로 결합법칙을 만족하고 a에 대한 항등원 0를 가지고 있기 때문에 (Z, +)는 모노이드에 속하는 대수구조이다.
④ 군(group)
대수구조 군은 역원을 갖는 모노이드이다. 즉, 집합과 집합 위에 결합법칙을 만족하는 이항연산이 정의되어 있고, 이항연산에 대해서는 항등원과 역원이 존재한다.
정수 집합 Z에 곱셈 연산으로 이루어진 대수구조 (Z, ×)는 군에 속하지 못한다. 정수 집합에 대해 곱셈 연산은 결합법칙을 만족하고 항등원 1도 가지고 있다. 하지만 정수 집합 원소 a의 역원 1/a는 정수 집합에 속하지 않으므로 대수구조 (Z, ×)는 모노이드에는 속하지만 군에는 속하지 않는 대수구조이다.
반면, 정수 집합 Z에 덧셈 연산으로 이루어진 대수구조 (Z, +)는 결합법칙을 만족하고, 임의의 정수 a에 대해서 항등원 1과 역원 (-a)가 모두 정수 집합에 속하므로 군에 속하는 대수구조이다.
⑤ 아벨군(abelian group)
대수구조 아벨군은 교환법칙이 성립하는 군이다. 즉, 집합과 집합 위의 결합법칙과 교환법칙을 만족하는 이항연산이 정의되어 있고, 이항연산에 대해서는 항등원과 역원이 존재한다.
정수 집합 Z에 대해서 덧셈 연산으로 이루어진 대수구조 (Z, +)는 아벨군에 속한다. 교환법칙, 결합법칙을 만족하고 항등원과 역원이 모두 존재한다. 또한 실수 집합 R에 대해서 곱셈 연산으로 이루어진 대수구조 (R, ×) 역시 아벨군에 속한다
⑥ 환(ring)
대수구조 환은 덧셈에 대하여 아벨군이 성립하고 곱셈에 대하여 반군을 이루며 분배법칙이 성립하는 대수구조이다. 반군, 모노이드, 군, 아벨군은 이항연산 하나에 대해서만 판단하였지만 환은 이항연산이 두 개 정의된다. 이를 표현상 덧셈, 곱셈이라고 하지만 다른 방식으로 정의하여도 문제는 없다. 따라서 대수구조는 하나의 연산(덧셈)에 대해서는 결합법칙과 교환법칙을 만족하고 항등원과 역원이 존재하며, 다른 연산(곱셈)에 대해서는 결합법칙만 만족하면 된다. 이항연산이 두 개 정의되었으므로 분배법칙 역시 만족해야 한다.
정수 집합 Z에 대해서 덧셈 연산과 곱셈 연산이 정의된 (Z, +, ×)는 환에 속한다. 정수 집합에 대해서 덧셈 연산은 아벨군의 조건을 만족한다. 또한 정수 집합에 대해서 곱셈 연산은 반군의 조건을 만족한다. 따라서 (Z, +, ×) 대수구조는 환에 속한다
⑦ 가군(module)
대수구조 가군은 환의 원소에 대한 곱셈이 정의된 아벨군이다. 즉, 집합과 집합 위에 결합법칙과 교환법칙을 만족하는 이항연산이 정의되어 있고, 이항연산에 대해서는 항등원과 역원이 존재한다. 여기에 추가로 환의 원소와 곱셈 연산이 정의되어 있는 대수구조이다.
가군이 중요한 이유는 선형대수학에서 다루는 벡터 공간이 가군에 속하기 때문이다. 벡터 공간과 가군의 차이는 가군은 환의 원소와 곱셈 연산이 정의되어 있지만 벡터 공간은 체의 원소와 곱셈 연산이 정의되어 있다. 벡터 공간에서 체의 원소와의 곱셈 연산은 스칼라 배와 관련이 있으며, 스칼라는 대수구조 체에 속하는 집합의 원소이다.
⑧ 가환환(commutative ring)
대수구조 가환환은 곱셈 연산이 교환법칙을 만족하는 환이다. 즉, 집합과 집합 위의 두 개의 이항연산이 정의되어 있으며, 하나의 이항연산(덧셈)은 교환법칙, 결합법칙을 만족하고 항등원과 역원이 있는 반면, 다른 하나의 이항연산(곱셈)은 교환법칙, 결합법칙을 만족한다. 또한 두 이항연산의 분배법칙도 성립한다.
⑧ 나눗셈환(division ring)
대수구조 나눗셈환은 0이 아닌 모든 원소가 역원을 가지며 원소의 개수가 둘 이상인 환이다. 즉 집합과 집합 위의 두 개의 이항연산이 정의되어 있으며, 하나의 이항연산(덧셈)은 교환법칙, 결합법칙을 만족하고 항등원과 역원이 있는 반면, 다른 하나의 이항연산(곱셈)은 결합법칙을 만족하고, 항등원과 0을 제외한 나머지 원소에 대해서 역원이 존재한다.
⑨ 체(field)
대수구조 체는 가환환이면서 나눗셈환인 대수구조이다. 즉 집합과 집합 위의 두 개의 이항연산이 모두 교환법칙과 결합법칙을 만족하고, 항등원과 0을 제외한 원손에 대해서 역원이 존재하는 대수구조이다. 대수구조 체에서는 사칙연산이 자유롭게 이루어질 수 있다.
'선형대수학' 카테고리의 다른 글
| 선형대수학: 03강 수학적 벡터 (3) - 여러 벡터공간 (0) | 2020.06.17 |
|---|---|
| 선형대수학: 03강 수학적 벡터 (2) - 벡터공간 (0) | 2020.06.16 |
| 선형대수학: 02강 물리적 벡터 (3) - 벡터의 응용 (0) | 2020.06.12 |
| 선형대수학: 02강 물리적 벡터 (2) - 벡터의 연산 (0) | 2020.06.12 |
| 선형대수학: 02강 물리적 벡터 (1) - 벡터와 좌표계 (0) | 2020.06.10 |


